エクセルExcelでΧ二乗検定を part3
かつては，
■ExcelでTukey法による多重比較
とか，
■フリードマンの検定をエクセルでなんとかする
といった，「お前，ちょっとニッチ過ぎにもほどがあるだろう」という記事を書いていた私ですが，少しは需要が高めな記事も書いていこうかと思ってきた今日この頃です．
以下の記事を読んでも不安がある場合や，元の作業ファイルで確認したい場合は，
このリンク先→「統計記事のエクセルのファイル」から，
「クロス集計によるχ二乗検定」
のエクセルファイルをダウンロードしてご確認ください．
さて，その「少しは需要が高め」なテーマですが，前回は，
■エクセルで相関係数のp値を出す
でした．
今回はカイ二乗検定です．
■エクセルExcelでΧ二乗検定を
■エクセルExcelでΧ二乗検定を part2
という記事を，遠い遠い遥か彼方に書いていたことがあります．
その続きです．
それではまず，例題であるデータから御覧ください．
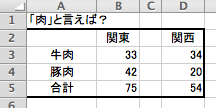
「肉」と言えば何肉ですか？
というアンケートをとったとして，それで関東と関西で回答結果を分けてみた，というものです．
関東は「豚肉」，関西では「牛肉」と回答する人が多いのだそうですよ．
この例題でも，なんか多分そんな感じではないかという印象ですね．
ではまずそれを，
■エクセルExcelでΧ二乗検定を
でご紹介したようにカイ二乗検定でｐ値を出してみましょう．
今回の記事では詳細は省いてササッといきます．
関西と関東でとった調査の合計（N数）から，期待値を算出します．
関東は「＝75 ÷ 2」で「37.5」，関西は「＝54 ÷ 2」で「27」を出しています．
そして，以下のようにカイ二乗検定をします．
すると・・・，
こんな結果になりました．
残念です．
ｐ値は，関西関東のいずれも「0.05」未満にはなりませんでした．
が，そもそも，このアンケートで調査したいのは，
地域によって回答パターンに違いが有るか否か？
という点です．
関東は関西よりも豚肉（関西は関東よりも牛肉）だと回答している人の数が多いのか？
という点を知りたいのですから，以下のような検定をします．
まずはデータ入力から．以下のようにします
ここでは，D列のところにも合計値を算出し，D列5行目には全回答数（総合計）も算出しておきます．
そして期待値の算出なのですが．
これはちょいとややこしいですが，以下のような計算をB列6行目に入れます．
=$D3*B$5/$D$5
「＄」マークを入れなくてもいいのですが，これを入れておけば，
こんなふうに，オートフィルでコピーできるので便利です．
手間がそんなに変わるわけじゃないので，各セルに打ち込んでいっても問題はありませんが．
つまりは，
上のような状態になればOK．
これが期待値になります．
で，この期待値を使ってカイ二乗検定にかけます．
=CHITEST(B3:C4,B6:C7)
それをD列9行目のところに入力してみました．
すると，
このように，ｐ値は「0.03345」と表示されました．
「0.05」未満ですので，これで晴れて，
「関東と関西で「肉と言えば，牛肉？豚肉？」と聞いた場合の回答パターンが異なる」
ということが言えるわけです．
良かった良かった．
ところが，それに
「ちょっと待ったー！！」
と言い出す人たちがいるかもしれません．中部地方の人たちです．
「肉といえば鶏肉だがやぁ」
ということで，以下の様なアンケートであればどうすればいいのでしょうか？
これも，まずは期待値を出すところから始めましょう．
=$E3*B$6/$E$6
と入力し，そしてこれをオートフィル．
これで期待値が算出されました．
その期待値を使って，F列9行目にカイ二乗検定の関数を入れています．
=CHITEST(B3:D5,B7:D9)
その算出結果がこれ．
「よーっし，有意だ．良かった良かった」
と思いきや，そこから先で悩む人がたくさんいます．
「何がどう有意なんだ？」というやつですね．
カイ二乗検定は「回答パターンに有意性が有る」ということを算出するものですから，行か列が３つ以上になると，どの回答結果によって有意性が出たのか分からなくなるのです．
これについて，SPSSでは「調整済み残差」というのを簡単に算出できて，それを見て判断できるのですけど．
というわけで，これをエクセルでやってみましょう．
※以下の例題に誤りがありました．2017年6月18日に訂正しています．
ご指摘くださった方に感謝申し上げます．
=(B3-B7)/SQRT(B7*(1-B$6/$E$6)*(1-B$6/$E$6))
＄マークは入力しなくてもいいですけど，こういうふうにしておくと（以下略
これ，どんな計算をしているのかというと，
＝ 実測値(B3のとこ) ― 期待値(B7のとこ)
で算出する「残差」を，それ以降の計算で調整してますよ，ということです．
毎度のことながら，詳しくは統計学の書籍にあたってください．
オートフィルで上の図のようになります．
これがSPSSでも出せる「調整済み残差」というやつです．
この調整済残差ですが，
「1.96以上，または，-1.96以下」のところに着目します．
なぜかって？それも統計学の書籍にあたってください．
例題では，以下のように1.96以上（-1.96以下）のところを赤字にしてみました．
この赤くなった部分は，
「期待（予測）よりも，数値が大きかった or 小さかったところ」です．
プラス値であれば「大きかった」，マイナス値であれば「小さかった」となります．
つまり，この例題のデータですと，
「肉と言えばなんですか？」と聞かれたとき，
（１）関東では「豚肉」と回答する人が関西・中部よりも多い
（２）関西では「牛肉」と回答する人が関東・中部よりも多く，「鶏肉」と回答する人は関東・中部よりも少ない
（３）中部では「牛肉」「豚肉」と回答する人が関東・関西よりも少なく，「鶏肉」と回答する人は関東・関西よりも多い．
ということを意味するのです．
ではまた，何かあれば追加していきたいと思います．
Amazon広告
その他，こういう怪しいブログ記事よりも，ちゃんと勉強になる書籍もご紹介しておきます．
詳しくは，
■独学で統計処理作業をスキルアップさせるための本
を御覧ください．
外部サイトにも有益なリストがあります．こちらも参考にしてください．
■大学生が自力で「統計学」の勉強をするための良書１０選
■1ヶ月で統計学入門したので「良かった本」と「学んだこと」のまとめ
■ExcelでTukey法による多重比較
とか，
■フリードマンの検定をエクセルでなんとかする
といった，「お前，ちょっとニッチ過ぎにもほどがあるだろう」という記事を書いていた私ですが，少しは需要が高めな記事も書いていこうかと思ってきた今日この頃です．
以下の記事を読んでも不安がある場合や，元の作業ファイルで確認したい場合は，
このリンク先→「統計記事のエクセルのファイル」から，
「クロス集計によるχ二乗検定」
のエクセルファイルをダウンロードしてご確認ください．
■エクセルで相関係数のp値を出す
でした．
今回はカイ二乗検定です．
■エクセルExcelでΧ二乗検定を
■エクセルExcelでΧ二乗検定を part2
という記事を，遠い遠い遥か彼方に書いていたことがあります．
その続きです．
それではまず，例題であるデータから御覧ください．
というアンケートをとったとして，それで関東と関西で回答結果を分けてみた，というものです．
関東は「豚肉」，関西では「牛肉」と回答する人が多いのだそうですよ．
この例題でも，なんか多分そんな感じではないかという印象ですね．
ではまずそれを，
■エクセルExcelでΧ二乗検定を
でご紹介したようにカイ二乗検定でｐ値を出してみましょう．
今回の記事では詳細は省いてササッといきます．
関東は「＝75 ÷ 2」で「37.5」，関西は「＝54 ÷ 2」で「27」を出しています．
そして，以下のようにカイ二乗検定をします．
残念です．
ｐ値は，関西関東のいずれも「0.05」未満にはなりませんでした．
が，そもそも，このアンケートで調査したいのは，
地域によって回答パターンに違いが有るか否か？
という点です．
関東は関西よりも豚肉（関西は関東よりも牛肉）だと回答している人の数が多いのか？
という点を知りたいのですから，以下のような検定をします．
まずはデータ入力から．以下のようにします
そして期待値の算出なのですが．
これはちょいとややこしいですが，以下のような計算をB列6行目に入れます．
「＄」マークを入れなくてもいいのですが，これを入れておけば，
手間がそんなに変わるわけじゃないので，各セルに打ち込んでいっても問題はありませんが．
つまりは，
これが期待値になります．
で，この期待値を使ってカイ二乗検定にかけます．
それをD列9行目のところに入力してみました．
すると，
「0.05」未満ですので，これで晴れて，
「関東と関西で「肉と言えば，牛肉？豚肉？」と聞いた場合の回答パターンが異なる」
ということが言えるわけです．
良かった良かった．
ところが，それに
「ちょっと待ったー！！」
と言い出す人たちがいるかもしれません．中部地方の人たちです．
「肉といえば鶏肉だがやぁ」
ということで，以下の様なアンケートであればどうすればいいのでしょうか？
と入力し，そしてこれをオートフィル．
その期待値を使って，F列9行目にカイ二乗検定の関数を入れています．
その算出結果がこれ．
と思いきや，そこから先で悩む人がたくさんいます．
「何がどう有意なんだ？」というやつですね．
カイ二乗検定は「回答パターンに有意性が有る」ということを算出するものですから，行か列が３つ以上になると，どの回答結果によって有意性が出たのか分からなくなるのです．
これについて，SPSSでは「調整済み残差」というのを簡単に算出できて，それを見て判断できるのですけど．
というわけで，これをエクセルでやってみましょう．
※以下の例題に誤りがありました．2017年6月18日に訂正しています．
ご指摘くださった方に感謝申し上げます．
=(B3-B7)/SQRT(B7*(1-B$6/$E$6)*(1-B$6/$E$6))
＄マークは入力しなくてもいいですけど，こういうふうにしておくと（以下略
これ，どんな計算をしているのかというと，
＝ 実測値(B3のとこ) ― 期待値(B7のとこ)
で算出する「残差」を，それ以降の計算で調整してますよ，ということです．
毎度のことながら，詳しくは統計学の書籍にあたってください．
これがSPSSでも出せる「調整済み残差」というやつです．
この調整済残差ですが，
「1.96以上，または，-1.96以下」のところに着目します．
なぜかって？それも統計学の書籍にあたってください．
例題では，以下のように1.96以上（-1.96以下）のところを赤字にしてみました．
「期待（予測）よりも，数値が大きかった or 小さかったところ」です．
プラス値であれば「大きかった」，マイナス値であれば「小さかった」となります．
つまり，この例題のデータですと，
「肉と言えばなんですか？」と聞かれたとき，
（１）関東では「豚肉」と回答する人が関西・中部よりも多い
（２）関西では「牛肉」と回答する人が関東・中部よりも多く，「鶏肉」と回答する人は関東・中部よりも少ない
（３）中部では「牛肉」「豚肉」と回答する人が関東・関西よりも少なく，「鶏肉」と回答する人は関東・関西よりも多い．
ということを意味するのです．
ではまた，何かあれば追加していきたいと思います．
関連記事
■アンケートだけで卒論・修論を乗り切るためのエクセルχ二乗検定Amazon広告
その他，こういう怪しいブログ記事よりも，ちゃんと勉強になる書籍もご紹介しておきます．
詳しくは，
■独学で統計処理作業をスキルアップさせるための本
を御覧ください．
外部サイトにも有益なリストがあります．こちらも参考にしてください．
■大学生が自力で「統計学」の勉強をするための良書１０選
■1ヶ月で統計学入門したので「良かった本」と「学んだこと」のまとめ
