注目の投稿
Steel-Dwass法をExcelで計算する方法について,もう少し詳細に
- リンクを取得
- ×
- メール
- 他のアプリ
昨日に引き続き,「スチューデント化された範囲の表」を使った多重比較ということで,Tukey-Kramer法の次はSteel-Dwass法です.




以前のSteel-Dwass法の記事である,
■ノンパラメトリック版Tukey法による多重比較「Steel-Dwass法」
で紹介した例ですと,以下のような問題点があります.
その記事の最後でも触れましたが,
(1)各群データの繰り返し数(N数)が一緒でなければいけない
(2)同順位のデータ(同じ値)はどのように処理・計算するのか?
というものです.
E = 片方のN数 × (総N数+1)÷2
外部サイトにも有益なリストがあります.こちらも参考にしてください.
■大学生が自力で「統計学」の勉強をするための良書10選
■1ヶ月で統計学入門したので「良かった本」と「学んだこと」のまとめ
手計算で算出するのが面倒な人は,思い切ってエクセル統計の購入をオススメします.




エクセルや手計算でTukeyやSteel-Dwassによる多重比較をしたい方は,以下の2冊がオススメです.
以前のSteel-Dwass法の記事である,
■ノンパラメトリック版Tukey法による多重比較「Steel-Dwass法」
で紹介した例ですと,以下のような問題点があります.
その記事の最後でも触れましたが,
(1)各群データの繰り返し数(N数)が一緒でなければいけない
(2)同順位のデータ(同じ値)はどのように処理・計算するのか?
というものです.
この点につき,Tukey法については,昨日の記事で「Tukey-Kramer法」を紹介することで解決しました.
今度はSteel-Dwass法の番です.
以下の記事を読んでも不安がある場合や,元の作業ファイルで確認したい場合は,
このリンク先→「統計記事のエクセルのファイル」から,
「Steel-Dwass法(異なるN数・同順位データの場合)」
のエクセルファイルをダウンロードしてご確認ください.
以下の記事を読んでも不安がある場合や,元の作業ファイルで確認したい場合は,
このリンク先→「統計記事のエクセルのファイル」から,
「Steel-Dwass法(異なるN数・同順位データの場合)」
のエクセルファイルをダウンロードしてご確認ください.
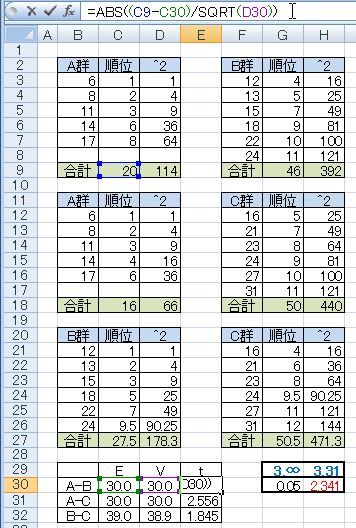
細かいところについては,上記に示している以前の記事を読んでもらうとして,今回扱うデータは以下の様なものです.
以前のデータを少し変えています.
B列とF列に各群の元データ,C列とG列にそれぞれの組み合わせにおける数値の順位を示しています.
そして,D列とH列に,それぞれの組み合わせにおける数値の順位を2乗した値を示しています.この数値とその合計は,あとで出てきますので.
ちなみに,上から順に,「A群とB群」「A群とC群」「B群とC群」を比較しています.
以前の記事のデータと違うのは,B群とC群のN数が「6個」になっていることと,B群とC群に同値のデータ「24」が入っていることです.
さて,
まず一点目,「データ数が群によって違う場合について」ですが,見てお分かりのように,気にせず順位を付けていけばOKです.
二点目の「同順位のデータの処理・計算」ですが,三段目の「B群とC群」のところに示したように,「24」を両方共「9.5」番目として処理しています.
9番目と10番目に相当するはずだった値ですから(この表現で分かりますか?),その間をとって「9.5」にしているのです.
先に5%での有意水準を計算しておきましょう.
これは前回と同様です.
「スチューデント化された範囲の表」を見て,3群で自由度は∞.「3.31」を使います.
そしてこの値を,今回の例でも
=H29/SQRT(2)
として「2.341」にしています.
※「スチューデント化された範囲の表」は,
などの記事から取ってきてください.
さて,これから各群を比較していくわけですが,上記の画像でいうと左側の表を完成させることで可能になります.
まず,「E」のところですが,
を計算します.
「片方のN数」といっても適当に群を選んではダメで,今回のような方法ですと,画像で言うところの左側の群の値を統一して使ってください.
「A群とB群」の組み合わせですと,
=5*(11+1)/2
です.
そんなふうにして,
A群とC群は,
=5*(11+1)/2
B群とC群は,
=6*(12+1)/2
と計算していきます.
次に「V」のところですが,ここが前回紹介したSteel-Dwass法と最も大きく異なるところでして,同順位の数値がなければ “あっち” の計算でもいいのですが,今回のように同順位があると,
V =
片方のN数 × もう一方のN数 ÷ 総N数(総N数-1) × (片方の順位を2乗した値の合計 + もう一方の順位を2乗した値の合計) - (総N数 × (総N数+1)^2÷4)
という長ったらしい計算をしなければなりません.
スマートに計算式だけで表すと,
です.
例で言うと,
A群とB群は,
=(5*6/(11*(11-1)))*((D9+H9)-(11*(11+1)^2/4))
A群とC群は,
=(5*6/(11*(11-1)))*((D18+H18)-(11*(11+1)^2/4))
B群とC群は,
=(6*6/(12*(12-1)))*((D27+H27)-(12*(12+1)^2/4))
最後に,Steel-Dwassの検定統計量(t)の計算です.
A群とB群は,
=ABS((C9-C30)/SQRT(D30))
A群とC群は,
=ABS((C18-C31)/SQRT(D31))
B群とC群は,
=ABS((C27-C32)/SQRT(D32))
です.
というわけで,以下が統計処理結果.
先に計算した5%水準である「2.341」よりも検定統計量(t)が大きいのはA群とC群を比較した「2.556」.
ここに有意性が認められた,ということになります.
※後日,こんな怪しいブログよりも信頼性が高いものに触れてもらうよう,
■独学で統計処理作業をスキルアップさせるための本
という記事を書きました.参照してください.■独学で統計処理作業をスキルアップさせるための本
外部サイトにも有益なリストがあります.こちらも参考にしてください.
■大学生が自力で「統計学」の勉強をするための良書10選
■1ヶ月で統計学入門したので「良かった本」と「学んだこと」のまとめ
手計算で算出するのが面倒な人は,思い切ってエクセル統計の購入をオススメします.
エクセルや手計算でTukeyやSteel-Dwassによる多重比較をしたい方は,以下の2冊がオススメです.
- リンクを取得
- ×
- メール
- 他のアプリ