注目の投稿
エクセルExcelでの簡単統計(相関関係)
- リンクを取得
- ×
- メール
- 他のアプリ
今回はひたすらExcelだけを使った相関関係についての統計処理です.
相関関係がどんなものか,簡単に説明しときます.
よく下の画像のような図を持ちだしてきて,
“xが大きくなればなるほど,yも大きくなる”
というような表現がされます.
1.解釈が簡単
2.視覚的にも訴えかけ易い
3.おまけにそのグラフを作る作業も楽
と三拍子そろっており,素人を騙すうえでも非常に強力なツールです.
研究やなんかでも多用される統計手法の一つで,とにかく解釈が簡単なうえに “いかようにも言い逃れできる” ところから,私としては最強の統計手法と位置づけています.
後日,その「最強の統計手法」を使って,最凶の卒論・修論作成法を解説しました.
■アンケートだけで卒論・修論を乗り切るためのエクセル相関関係
悪用しないようにご活用ください.
実際,適当な研究報告書とか説明資料をつくる時には重宝します.しかも相関関係を表す図は大きくなりやすいことから,ページ数を稼ぐ力もありますのでまさに言うこと無しですね.
マジメな話,それだけに解釈の仕方には十分に気を付けなければならない統計手法です.
・二酸化炭素が増加すると気温が高くなる
・警察官が多い都市ほど犯罪が多い
・お小遣いが多いお父さんほど給料が高い
なんていう統計おもしろネタは多いものです.
※これらは全て逆から読んだほうが正しい解釈の可能性が高い
でも,これらを本気で信じちゃう人もいるので注意しなきゃいけないのです.
前置きはこれぐらいで,さっそくExcelの操作方法です.
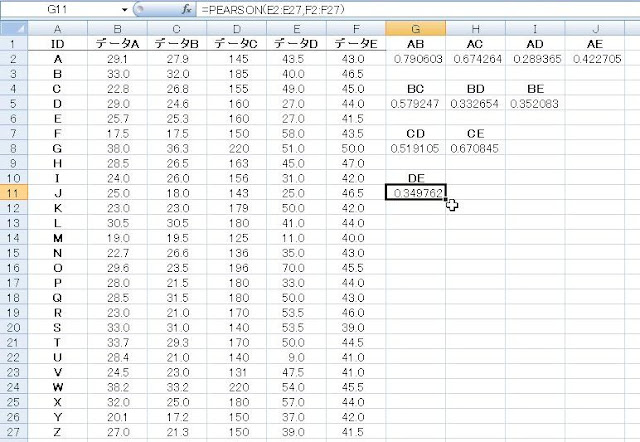
下に示した図のようなデータが典型的な例でしょうか.
では相関関係を示す統計処理として有名なピアソンの積率相関係数というのを出しましょう.
G列2行目のセルに以下の関数を入力し,データAとデータBの相関関係を求めます.
=PEARSON(B2:B27,C2:C27)
以上,基本的にはこれで相関係数の算出は終了です.
このあと,このままセルをオートフィルで右方向にひっぱって自動的に算出してもいいのですが.
私は以下の図のように,どことどこを参照しているのかタイトルを付けておいて,$マークを使って参照元を固定しながら(この場合データAであるB列を固定),
そしてオートフィルします.
この調子で全部の組み合わせをやっていきます.
今回の例のデータはA~Eの5つですが,処理しなければいけないものによっては10も20もある場合があります.
そうなると1組ずつ関数を入力してたら疲れますので,このオートフィルで楽しましょう.
上記の説明を読んで何がなんだかわからない人は,Excelの使い方をググッてください.
データが10も20もある場合は,先の例に出したように右方向にずっと組み合わせを並べていくと途方もない長さになります.
以下のように並べ変えておくとよいでしょう.
このようにすれば,結果が見やすいですし,作業も横スクロールが少なくて済みます.
と,ここまではウォーミングアップです.
もっとパパっと相関係数を求める方法があります.ちょっと慣れないと手間ですが,相関係数をだすだけなら,この方法が楽だと思います.
前回の記事で扱ったアドインによる 「分析ツール」 のなかに 「相関」 という分析機能があります.これを利用する方法です.
※分析ツールのアドインについては別に調べてください.
以下が分析ツールの中にある相関です.
(ちなみに,これはExcel2007を使用した説明です)
このなかにある 「相関」 を選択した状態でOKをクリックします.
すると以下のような画面が出ますので,
入力範囲の右端にある赤青白のマーク部分をクリックして,選択範囲としてB列2行目~F列27行目までを選択します.
そしてさっきの画面に戻るので,データ方向が「列」になっていることと,出力オプションで「新規ワークシート」になっていることを確認してOKをクリックします.
すると以下のような新規ワークシートが出現し,一気に全ての組み合わせの相関係数を見ることができます.
列1というのはデータAのこと,データEは列5です.
というわけで,分析ツールをつかった相関係数の求め方は以上です.
最後に,大量のデータを一気に扱うことはできないけど,もっとお手軽に相関係数を求める方法というのを説明します.
まず,データAとデータBによる散布図を作成します.
散布図作成は端折っていきますが,以下のようにしてデータ範囲を選択し,
挿入タブからグラフの散布図を選択し,
以下のように散布図を作成します.
そして今度は,散布図の点々を右クリックするなどして「近似曲線の追加」を行ないます.
以下のような画面がでるので,四の五の言わずに 「グラフにR-2乗値を表示する」 にチェックを入れて「閉じる」をクリック.
そしたら,以下のようにグラフ中にR2乗値がでます.0.6251と出ていますね.
(わかりやすいようにフォントを大きくする修正をしています)
出てきたこの「R2乗値」ですが,これを手元にある電卓とかWindowsのアクセサリにある電卓機能などで平方根を返すと,
0.7906.....
という数値が出ます.
さっき関数や分析ツールで算出した,データAとデータBの相関係数と比べてみてください.
四捨五入の関係で若干数値が違いますが,ぴったり合っているはずです.
逆に,データAとデータBの相関係数である0.790603を二乗してみてください.
0.62505....
ということで四捨五入すれば0.6251になります.
散布図の近似曲線のところで追加できるR2乗値,実は平方根を返せばピアソンの積率相関係数と同じ値になるのです.
この方法の良いところは,
「この組み合わせの相関係数を知りたいだけなんだよなぁ」
という場合に,グラフを作成しながら確認できることです.
「この組み合わせの相関係数を知りたいだけなんだよなぁ」
という場合に,グラフを作成しながら確認できることです.
案外利用価値は高いですよ.
例えば,大至急にミーティング資料や報告書用にグラフを作成しているという時に,その相関係数はどれくらいなのかという確認をチャチャッとやりたい場合,作業を並行しながら行えるという特長があります.
ちなみに相関係数を2乗した数値のことを「決定係数」といいます.
決定係数についてはまた別の機会にしますが,そういうものがある,ということで覚えといてください.
ところで,求めた相関係数が有意かどうかの確認はどうすればいいか?
という疑問があるかと思います.
SPSSとかエクセル統計なんかの統計ソフトには相関係数だけでなく,その相関係数が有意かどうかのP値も一緒に出てきます.
でも,この相関係数が有意かどうかの算出はめんどくさい上に,その確認は「相関係数の棄却限界」を示した表が出回っているので,やらない人が多いです.
というわけで,以下にその相関係数の棄却限界の表を示します.
例えば,例として出したデータAとBの相関係数が5%水準で有意かどうかを知りたければ,表中の対象数26(自由度24)の5%のところを見ます.
すると,「0.388」ですね.
この数値よりも相関係数が大きければ有意ということなのです.
データAとBの相関係数が0.790603ですので,有意ということになります.
ただ,これは統計学上で有意な相関というだけで,0.6~0.7以上の相関係数がなければ「関係がありそうだ」とは言えない気がします(私的に).
体力測定などの信頼性を評価するのであれば0.8以上が必要な気もしますし,精密測定機器であれば0.999...(限りなく1)が求められたりするでしょう.
相関係数の解釈について,こればっかりはこの記事1本で説明は無理です.あらためて記事にします.
早く知りたい,納得したい人もいるかと思います.
こういったことは本を読んで勉強してください.
D・ロウントリー 著 『新・涙なしの統計学』 や 田中喜代次/西嶋尚彦 監訳 『身体活動学における研究方法』とかを参考にしてみてください.
次回は,この相関係数に差があるかどうか?を検定する方法を取り上げます.
意外と学生から質問が多いのが,この相関係数の差の検定なもので.
外部サイトにも有益なリストがあります.こちらも参考にしてください.
■大学生が自力で「統計学」の勉強をするための良書10選
■1ヶ月で統計学入門したので「良かった本」と「学んだこと」のまとめ
信頼性係数はこちら↓
■信頼性係数をエクセルで算出する
Amazon広告












意外と学生から質問が多いのが,この相関係数の差の検定なもので.
※後日,こんな怪しいブログよりも信頼性が高いものに触れてもらうよう,
■独学で統計処理作業をスキルアップさせるための本
という記事を書きました.参照してください.■独学で統計処理作業をスキルアップさせるための本
外部サイトにも有益なリストがあります.こちらも参考にしてください.
■大学生が自力で「統計学」の勉強をするための良書10選
■1ヶ月で統計学入門したので「良かった本」と「学んだこと」のまとめ
信頼性係数はこちら↓
■信頼性係数をエクセルで算出する
Amazon広告