注目の投稿
アンケートだけで卒論・修論を乗り切るためのエクセル相関関係
- リンクを取得
- ×
- メール
- 他のアプリ
アンケートだけで卒論・修論を乗り切る統計シリーズ.
記事のシリーズには,現在,
■アンケートだけで卒論・修論を乗り切るためのエクセルt検定
■アンケートだけで卒論・修論を乗り切るためのエクセルχ二乗検定
■アンケートだけで卒論・修論を乗り切るためのエクセルで相関係数の差を検定する方法
があります.
今回は相関関係と,相関係数を用いた分析方法です.
卒論や修論のテーマを頑張って考えてみたけど,ぜんぜん思いつかない.
そのまま時は過ぎ,気がつけば論文を書き始めなきゃいけないボーダーラインまで来てしまった,という学生のためのシリーズとなっています.
目次はこちら
(1)相関関係の示し方
今回お示ししているデータの元になっているエクセル・ファイルが欲しい人は,
このリンク先→「統計記事のエクセルのファイル」から,
「相関関係について」
「その他・目的別」
のところにある該当するファイルをダウンロードしてご確認ください.
なんと言っても,グラフ「散布図」にすることでページ数が稼げます.
以下のようなグラフです.見たことがある学生も多いでしょう.
横軸と縦軸の関係性を示すことで,「Xが大きくなれば,Yも大きくなる」といったシンプルな主張を展開することができ,考察が比較的簡単です.
しかも,このグラフは情報量が少ない割に紙面の縦幅をとります.
ですので,ページ数が稼ぎやすくなります.
逆に,ページ数を増やしたくない場合は,グラフにせずに「表」にすれば紙面を節約することになりますので,使い勝手がいい分析方法と言えます.
とりあえず早く卒論を提出して楽になりたい学生にとっては,強い味方です.
(1)関係性を調べたい,2つのデータが必要
(2)その2つのデータは,いずれも同じ条件下で得られたもの(アンケートであれば,同じ集団から聞き取られた回答データであること)
(3)その2つのデータは,いずれも変量(性質を数値で表したもの)であること(男性・女性や,YES・NOといった回答データは相関関係の分析には使えない)
ここで何を言っているのか分からない.という学生も多いと思います.
統計学の授業や,ゼミで先生が何を言っていたか聞いている人なら何とかなりますが,そもそも,こんなネット記事を探している時点で「聞いていなかった」のでしょう.
きっと統計学の教科書も読んでいないはず.
実際に,以下のようにデータを入力しながら確認してください.
たとえば,こんな調査データがあったとします↓
ある大学の学生たちの成績です.
このデータで「相関関係」が分析できるのは,基礎科目,応用科目,共通科目,下宿先家賃の4つです.
「性別」はもちろんできませんし,「学年」もできません.
これは調査対象のカテゴリ(属性)のデータですので,相関関係を求めることはできないのです.
これらを分析したい場合は,相関関係ではなく「t検定」や「カイ二乗検定」などを用います.
■アンケートだけで卒論・修論を乗り切るためのエクセルt検定
■アンケートだけで卒論・修論を乗り切るためのエクセルχ二乗検定
たとえば,以下のような感じで,性別で点数の平均値を比較するなどです.
一方,基礎科目,応用科目,共通科目の点数と,下宿先の家賃の場合は相関関係が分析できます.
この中から2つのデータを使って
ためしに,「基礎科目と応用科目の点数の相関関係」を作ってみました.
相関関係の分析には「散布図」を作成することが便利です.
散布図の作成方法は,エクセルのバージョンやOSによって異なるので割愛します.ググってください.
このように,片方の点数が大きければ,もう片方の点数も大きくなる場合を「正の相関」と言います.
例データとしては,「基礎科目の成績が高い学生は,応用科目の成績も高い」と言えます.
次に,「応用科目と共通科目の点数の相関関係」を作ってみました.
今度は,右肩下がりの点々が打たれました.
一方の点数が大きければ,もう一方の点数が小さくなる場合を「負の相関」と言います.
例データとしては,「応用科目の成績が高い学生は,共通科目の成績が低い」と言えます.
次に,「基礎科目の点数と下宿先家賃の相関関係」です.
元々のデータの中には「自宅通い」というものがありましたが,それを入れたままだと正しく散布図が描けません.
そこで,相関関係の分析と散布図を作成するにあたって,「自宅通い」という入力データを削除しました.これにより,散布図が作成できます.
なお,この分析を論文で示す場合には,「自宅通いの者はデータから除外した」などと説明しておく必要があります.
以上,このようにして,任意の2つのデータの相関関係を示していくわけですが・・・.
これだけでは「相関関係の分析」としては不十分です.
グラフを見せて,「ほら,この値が大きい者は,もう一方の値も大きいでしょ?」と説明しても,それは感覚的・主観的なものでしかありません.
統計学的に示す必要が出てきます.
そのために,相関係数の算出が必要になります.
【方法1】 散布図の「R二乗値」から相関係数を算出する
ある意味で,もっとも手軽な方法からご紹介します.
まず,先ほど作った「散布図」で,「R二乗値」を算出していました.
この部分です.
「R-2 = 0.8391」と表示されているところです.
これは,ほとんどのバージョンのエクセルで,グラフ上のデータを示す「点々」を選択したのち,それを右クリックした際に出てくる以下の「近似曲線の追加」で出すことができます.

この「R^2」の平方根をとれば,それが「相関係数」です.
今回のデータ例であれば,
R^2= 0.8391
ですので,電卓やエクセル上で平方根をとれば「0.916」が出てきます.
エクセル上で計算してみます.
ここでは,A列28行目に,「0.8391」を入力しました.
そして,C列28行目に,その平方根をとる関数「SQRT」を使って算出します.
C列28行目には,
=SQRT(A28)
と入力しました.
その結果,0.91602と算出されました.
なお,応用科目と共通科目のR^2は,「0.3164」でしたから,「0.5624」となります.
R2乗値でもいいのですが,一般的に「相関関係」を示すためには「相関係数(ピアソンの積率相関係数と呼ばれます)」を算出することが多いので,こちらを使ってください.
相関係数はアルファベット小文字の「r(アール)」で示しますので,
「r = 0.916」や,「r = 0.562」と書きます.
なお,数字は小数点第二位や三位くらいで四捨五入してください.
【方法2】エクセルの関数「PEARSON」もしくは「CORREL」で算出する
もう一つの方法.こっちの方が一般的な算出方法です.
エクセルには,「相関係数」を算出する関数があります.
「基礎科目と応用科目の相関係数」を算出するのであれば,以下のように,その該当するデータ部分を「PEARSON」または「CORREL」の関数で参照します.
データ例の場合,D列13行目のところに,
=PEARSON(D3:D11,E3:E11)
と入力しました.
もしくは,「CORREL」関数でも算出できます.
=CORREL(D3:D11,E3:E11)
その結果がこちらです.
上述した【方法1】と同じになります.
以上で,相関係数が算出できました.
しかし,これだけではまだ不十分です.
この「0.916」とか「0.562」といったr値が,統計学的に有意かどうかを示す必要もあります.
しかし,統計学の教科書が今現在手元にない,5%水準とかの意味が分からない,解説を読むのも面倒くさい,という学生は,以下の方法で算出してください.
方法は過去記事の,
■エクセルで相関係数のp値を出す
に書きましたので,詳しい解説はそちらをどうぞ.
ここでは,上記までの流れから算出例をご紹介します.
上述してきた方法により,r値が算出できたとしましょう.
例として,「基礎科目と応用科目の相関係数」を使います.
そのr値を使って,以下のような「t値」を算出します.
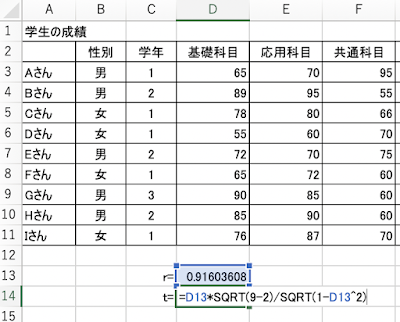
このデータでは,D列13行目に算出したr値を使って,D列14行目に,
=D13*SQRT(9-2)/SQRT(1-D13^2)
の式を入れています.
これにより,「t値(ティーち)」が出せます.
この式は,
=相関係数 × SQRT(N数 − 2) ÷ SQRT(1 − 相関係数の二乗)
を意味しています.
例では「9−2」になっている「N数−2」の部分は,9人のデータを使っているからです.
「−2」というのは,どのようなデータでも必ず「−2」になります.
もし,100人のデータを使えば,「100−2」です.
次に,このt値を使って,「p値(ピーち)」を出します.
D列15行目のところに,
=TDIST(D14,7,2)
と入力しています.
後ろの方にある,数字の「7」とか「2」について解説します.
「自由度」を意味する部分「7」は,前述したt値を出す際の「N数−2」の数字と同じ意味です.
この例であれば9人のデータですから,「9−2」で7です.
もし100人のデータであれば,「100−2」で98になります.
最後の数字である「2」は,ほとんどすべての調査や論文で「2」を使います.
詳しくは統計学の教科書を読んでほしいのですが,面倒なら「2」にしておけばOKです.
これにより,p値が算出できます.
算出結果は「p = 0.00051984」となっています.
このp値は,「0.05未満」であれば統計学的に有意である.つまり,
「基礎科目の成績が良い学生は応用科目も良い(基礎科目の成績が悪い学生は,応用科目も悪い)」
と解釈できることを意味します.
一方で,このp値が「0.05以上」あると,グラフ上では相関関係があるように見えても,そのように解釈することはできないのです.
これで相関関係の分析はバッチリです.
【注意!】
ちなみに,この算出方法を「負の相関」のところでも同じように出そうとすると,エラーになりますので注意しましょう.
例えば,今回の例データであれば「応用科目と共通科目の相関係数」はマイナスの値「負の相関」になります.
それでt値を出すと,マイナスの値になります.
それを使ってp値を出すと,#NUM!となります.
この場合,t値からマイナスをとる(絶対値を使う)必要があります.
マイナスをとる関数として,指定した数値を絶対値にする「ABS」があります.
なので,以下のようにします.
p値を出す「TDIST」関数のところで,「D14」の前にABS関数を入れました.
=TDIST(ABS(D14),7,2)
これにより,t値を絶対値にできますので,以下のような結果が得られます.
p値がエラー無く算出できました.
しかし,このp値をみてもらうと,「0.05以上」の数値であることが分かります.
ということは,
「応用科目の成績が良い学生は,共通科目の成績が悪い(応用科目の成績が悪い学生は,共通科目の成績が良い)」
とは言えないことを意味します.
そこに見えていた以下のような散布図の関係性は,実は感覚的なものであって,統計学的に意味が有る(有意)とは言えないのです.
いずれもp値は0.05未満で有意です.
これらを一緒にして「有意でした」,で済ますだけではもったいない気がします.
つまり,1回目のテストで「20」だったけど,2回目のテストでは「15」や「25」を示すテスト方法ということになります.
もっと詳しく知っておきたい人や,用語がよく分からなくて困った人,もうちょっと高度なことがしたいという人は,以下の書籍を買ったり図書館で見つけて読んでください.
手計算で算出するのが面倒な人は,思い切ってエクセル統計の購入をオススメします.
関連記事
■アンケートだけで卒論・修論を乗り切るためのエクセルt検定
■アンケートだけで卒論・修論を乗り切るためのエクセルχ二乗検定
■エクセル散布図で相関係数・相関係数を確認する便利な方法
■エクセルでの簡単統計(相関関係)
記事のシリーズには,現在,
■アンケートだけで卒論・修論を乗り切るためのエクセルt検定
■アンケートだけで卒論・修論を乗り切るためのエクセルχ二乗検定
■アンケートだけで卒論・修論を乗り切るためのエクセルで相関係数の差を検定する方法
があります.
今回は相関関係と,相関係数を用いた分析方法です.
卒論や修論のテーマを頑張って考えてみたけど,ぜんぜん思いつかない.
そのまま時は過ぎ,気がつけば論文を書き始めなきゃいけないボーダーラインまで来てしまった,という学生のためのシリーズとなっています.
目次はこちら
(1)相関関係の示し方
(2)相関係数を算出する
(3)相関係数の有意性を算出する
(4)相関係数の強さを判別する
今回お示ししているデータの元になっているエクセル・ファイルが欲しい人は,
このリンク先→「統計記事のエクセルのファイル」から,
「相関関係について」
「その他・目的別」
のところにある該当するファイルをダウンロードしてご確認ください.
(0)アンケート調査における相関関係の強み
処理方法が知りたいだけの人は,(1)相関関係の示し方 まで飛ばしてください.なんと言っても,グラフ「散布図」にすることでページ数が稼げます.
以下のようなグラフです.見たことがある学生も多いでしょう.
横軸と縦軸の関係性を示すことで,「Xが大きくなれば,Yも大きくなる」といったシンプルな主張を展開することができ,考察が比較的簡単です.
しかも,このグラフは情報量が少ない割に紙面の縦幅をとります.
ですので,ページ数が稼ぎやすくなります.
逆に,ページ数を増やしたくない場合は,グラフにせずに「表」にすれば紙面を節約することになりますので,使い勝手がいい分析方法と言えます.
とりあえず早く卒論を提出して楽になりたい学生にとっては,強い味方です.
(1)相関関係の示し方
相関関係を分析するためのデータには,以下の条件があります.(1)関係性を調べたい,2つのデータが必要
(2)その2つのデータは,いずれも同じ条件下で得られたもの(アンケートであれば,同じ集団から聞き取られた回答データであること)
(3)その2つのデータは,いずれも変量(性質を数値で表したもの)であること(男性・女性や,YES・NOといった回答データは相関関係の分析には使えない)
ここで何を言っているのか分からない.という学生も多いと思います.
統計学の授業や,ゼミで先生が何を言っていたか聞いている人なら何とかなりますが,そもそも,こんなネット記事を探している時点で「聞いていなかった」のでしょう.
きっと統計学の教科書も読んでいないはず.
実際に,以下のようにデータを入力しながら確認してください.
たとえば,こんな調査データがあったとします↓
ある大学の学生たちの成績です.
このデータで「相関関係」が分析できるのは,基礎科目,応用科目,共通科目,下宿先家賃の4つです.
「性別」はもちろんできませんし,「学年」もできません.
これは調査対象のカテゴリ(属性)のデータですので,相関関係を求めることはできないのです.
これらを分析したい場合は,相関関係ではなく「t検定」や「カイ二乗検定」などを用います.
■アンケートだけで卒論・修論を乗り切るためのエクセルt検定
■アンケートだけで卒論・修論を乗り切るためのエクセルχ二乗検定
たとえば,以下のような感じで,性別で点数の平均値を比較するなどです.
一方,基礎科目,応用科目,共通科目の点数と,下宿先の家賃の場合は相関関係が分析できます.
この中から2つのデータを使って
ためしに,「基礎科目と応用科目の点数の相関関係」を作ってみました.
相関関係の分析には「散布図」を作成することが便利です.
散布図の作成方法は,エクセルのバージョンやOSによって異なるので割愛します.ググってください.
例データとしては,「基礎科目の成績が高い学生は,応用科目の成績も高い」と言えます.
次に,「応用科目と共通科目の点数の相関関係」を作ってみました.
今度は,右肩下がりの点々が打たれました.
一方の点数が大きければ,もう一方の点数が小さくなる場合を「負の相関」と言います.
例データとしては,「応用科目の成績が高い学生は,共通科目の成績が低い」と言えます.
次に,「基礎科目の点数と下宿先家賃の相関関係」です.
元々のデータの中には「自宅通い」というものがありましたが,それを入れたままだと正しく散布図が描けません.
そこで,相関関係の分析と散布図を作成するにあたって,「自宅通い」という入力データを削除しました.これにより,散布図が作成できます.
なお,この分析を論文で示す場合には,「自宅通いの者はデータから除外した」などと説明しておく必要があります.
以上,このようにして,任意の2つのデータの相関関係を示していくわけですが・・・.
これだけでは「相関関係の分析」としては不十分です.
グラフを見せて,「ほら,この値が大きい者は,もう一方の値も大きいでしょ?」と説明しても,それは感覚的・主観的なものでしかありません.
統計学的に示す必要が出てきます.
そのために,相関係数の算出が必要になります.
(2)相関係数を算出する
エクセルで相関係数を求める方法は,以下の通りです.【方法1】 散布図の「R二乗値」から相関係数を算出する
ある意味で,もっとも手軽な方法からご紹介します.
まず,先ほど作った「散布図」で,「R二乗値」を算出していました.
この部分です.
 |
これは,ほとんどのバージョンのエクセルで,グラフ上のデータを示す「点々」を選択したのち,それを右クリックした際に出てくる以下の「近似曲線の追加」で出すことができます.
ここをクリックすると,エクセル for Macであれば,以下のような画面が右端に出てきます.
その一番下の「グラフにR-2乗値を表示する」という部分にチェックを入れれば,その「R-2乗値」をグラフ上に乗せることができます.

この「R^2」の平方根をとれば,それが「相関係数」です.
今回のデータ例であれば,
R^2= 0.8391
ですので,電卓やエクセル上で平方根をとれば「0.916」が出てきます.
エクセル上で計算してみます.
ここでは,A列28行目に,「0.8391」を入力しました.
そして,C列28行目に,その平方根をとる関数「SQRT」を使って算出します.
C列28行目には,
=SQRT(A28)
と入力しました.
その結果,0.91602と算出されました.
なお,応用科目と共通科目のR^2は,「0.3164」でしたから,「0.5624」となります.
R2乗値でもいいのですが,一般的に「相関関係」を示すためには「相関係数(ピアソンの積率相関係数と呼ばれます)」を算出することが多いので,こちらを使ってください.
相関係数はアルファベット小文字の「r(アール)」で示しますので,
「r = 0.916」や,「r = 0.562」と書きます.
なお,数字は小数点第二位や三位くらいで四捨五入してください.
【方法2】エクセルの関数「PEARSON」もしくは「CORREL」で算出する
もう一つの方法.こっちの方が一般的な算出方法です.
エクセルには,「相関係数」を算出する関数があります.
「基礎科目と応用科目の相関係数」を算出するのであれば,以下のように,その該当するデータ部分を「PEARSON」または「CORREL」の関数で参照します.
データ例の場合,D列13行目のところに,
=PEARSON(D3:D11,E3:E11)
と入力しました.
もしくは,「CORREL」関数でも算出できます.
=CORREL(D3:D11,E3:E11)
その結果がこちらです.
上述した【方法1】と同じになります.
以上で,相関係数が算出できました.
しかし,これだけではまだ不十分です.
この「0.916」とか「0.562」といったr値が,統計学的に有意かどうかを示す必要もあります.
(3)相関係数の有意性を算出する
「相関係数の有意性」は,統計学の教科書の最後の方のページに載っている「相関係数の棄却限界の表」を使えば有意水準を「5%水準:0.05」とか「0.1%水準:0.001」などで判別できます.しかし,統計学の教科書が今現在手元にない,5%水準とかの意味が分からない,解説を読むのも面倒くさい,という学生は,以下の方法で算出してください.
方法は過去記事の,
■エクセルで相関係数のp値を出す
に書きましたので,詳しい解説はそちらをどうぞ.
ここでは,上記までの流れから算出例をご紹介します.
上述してきた方法により,r値が算出できたとしましょう.
例として,「基礎科目と応用科目の相関係数」を使います.
そのr値を使って,以下のような「t値」を算出します.
このデータでは,D列13行目に算出したr値を使って,D列14行目に,
=D13*SQRT(9-2)/SQRT(1-D13^2)
の式を入れています.
これにより,「t値(ティーち)」が出せます.
この式は,
=相関係数 × SQRT(N数 − 2) ÷ SQRT(1 − 相関係数の二乗)
を意味しています.
例では「9−2」になっている「N数−2」の部分は,9人のデータを使っているからです.
「−2」というのは,どのようなデータでも必ず「−2」になります.
もし,100人のデータを使えば,「100−2」です.
次に,このt値を使って,「p値(ピーち)」を出します.
D列15行目のところに,
=TDIST(D14,7,2)
と入力しています.
後ろの方にある,数字の「7」とか「2」について解説します.
「自由度」を意味する部分「7」は,前述したt値を出す際の「N数−2」の数字と同じ意味です.
この例であれば9人のデータですから,「9−2」で7です.
もし100人のデータであれば,「100−2」で98になります.
最後の数字である「2」は,ほとんどすべての調査や論文で「2」を使います.
詳しくは統計学の教科書を読んでほしいのですが,面倒なら「2」にしておけばOKです.
これにより,p値が算出できます.
算出結果は「p = 0.00051984」となっています.
このp値は,「0.05未満」であれば統計学的に有意である.つまり,
「基礎科目の成績が良い学生は応用科目も良い(基礎科目の成績が悪い学生は,応用科目も悪い)」
と解釈できることを意味します.
一方で,このp値が「0.05以上」あると,グラフ上では相関関係があるように見えても,そのように解釈することはできないのです.
これで相関関係の分析はバッチリです.
【注意!】
ちなみに,この算出方法を「負の相関」のところでも同じように出そうとすると,エラーになりますので注意しましょう.
例えば,今回の例データであれば「応用科目と共通科目の相関係数」はマイナスの値「負の相関」になります.
それでt値を出すと,マイナスの値になります.
それを使ってp値を出すと,#NUM!となります.
この場合,t値からマイナスをとる(絶対値を使う)必要があります.
マイナスをとる関数として,指定した数値を絶対値にする「ABS」があります.
なので,以下のようにします.
p値を出す「TDIST」関数のところで,「D14」の前にABS関数を入れました.
=TDIST(ABS(D14),7,2)
これにより,t値を絶対値にできますので,以下のような結果が得られます.
p値がエラー無く算出できました.
しかし,このp値をみてもらうと,「0.05以上」の数値であることが分かります.
ということは,
「応用科目の成績が良い学生は,共通科目の成績が悪い(応用科目の成績が悪い学生は,共通科目の成績が良い)」
とは言えないことを意味します.
そこに見えていた以下のような散布図の関係性は,実は感覚的なものであって,統計学的に意味が有る(有意)とは言えないのです.
(4)相関係数の強さを判別する
有意性を算出したら,次はr値の解釈についてです.
p値を見て,0.05未満であれば「有意」として判断するのもいいですが,算出した相関係数の「強さ」も分析することもできます.
相関係数は,「1(−1)」が最も強い(完全な)相関であり,「0」が無相関として解釈されています.
ですから,「r = 0.791」と「r = 0.423」という2つの相関係数があり,両者ともp値が0.05未満であっても,散布図にした時のグラフの形が違います.
例えば,以下のように.
Aのグラフは「 0.791 」,
Bのグラフは「 0.423 」ですが,いずれもp値は0.05未満で有意です.
これらを一緒にして「有意でした」,で済ますだけではもったいない気がします.
そこで,一般的に「相関係数の強さ」を判別する基準が普及しています.
 |
| Guilfordによる基準 |
これを参照してもらえれば,Aのグラフは「強い相関がある」と言えますし,Bのグラフは「中程度の相関がある」と評価できます.
しかし,r値の強さの解釈には注意が必要ですので,その話を最後にしておきます.
実は,こうした「r値(相関係数)の強さの目安・基準値」というのは,ほとんど意味がありません.
r値が強い/弱いの判断は,「一般的な基準値」では判断できないのです.
それは,研究領域や調査内容や実験内容によってまったく異なるからです.
例えば,以下のグラフをご覧ください.
「テスト方法X」というテストを2回行った測定値を散布図にしたものです.
このデータによる相関係数(r値)は「0.90」で,p値も0.05未満の有意な相関関係です.
「r = 0.90」というのは,非常に強い相関があると考えられますが,必ずしもそうとは言えません.
相関係数が「1」もしくは「−1」ではない限り,そこにはバラツキがあります.
1回目のテスト(横軸)の「20」という部分を上にたどってみてください.
その直線上には2つの点が打たれていますよね.
2回目のテスト(縦軸)の「15」と「25」です.
つまり,1回目のテストで「20」だったけど,2回目のテストでは「15」や「25」を示すテスト方法ということになります.
もしここで言う「テスト方法X」が,「物の長さを測る測定装置」で,単位が「m」だったらどうでしょうか?
その測定装置は,同じ物体を測っても,15mと表示されるかもしれないし,25mと表示されるかもしれない装置ということになります.
そんな測定装置を「非常に強い相関がある」と評価して良いのか? かなり疑問に思うでしょう.
しかし,だいたいの長さが分かればいい現場での装置だとか,km規模の長さを測る装置で,この単位が「mm」であれば話は変わってきます.
ですから,相関係数そのものだけで「強い/弱い」と評価するのは,ほとんど意味がないのです.
では,その相関係数の強さをどのように判断すればいいのか?
それこそ,指導教員に尋ねるのがいいでしょう.そのための指導教員だと思います.
もし「それを考えるのが卒論だ!」と怒られて突っぱねられたら,君は一目置かれたと思って喜ぶべきです.
なお,上記のデータのような再現性や信頼性に関する統計手法については,
で詳しく解説しています.
もっと詳しく知っておきたい人や,用語がよく分からなくて困った人,もうちょっと高度なことがしたいという人は,以下の書籍を買ったり図書館で見つけて読んでください.
手計算で算出するのが面倒な人は,思い切ってエクセル統計の購入をオススメします.
関連記事
■アンケートだけで卒論・修論を乗り切るためのエクセルt検定
■アンケートだけで卒論・修論を乗り切るためのエクセルχ二乗検定
■エクセル散布図で相関係数・相関係数を確認する便利な方法
■エクセルでの簡単統計(相関関係)