ウィルコクソンの符号付順位和検定（エクセルでp値を出す）
前回はマン・ホイットニーのU検定でしたので，今度は対応のある2群間の検定ということで，ウィルコクソン（Wilcoxon）の符号付き順位和検定をやります．
ウィルコクソンの符号付き順位和検定ですが，私にとっては思い入れのある検定方法でして．
卒業論文の統計処理に採用した，私の論文初の検定方法です．
パラメトリック検定では有意性が認められないから 「どーしよー・・・」 と悩んでおり，指導教員の言われるがままにノンパラメトリック検定に鞍替えすることに．
マッキントッシュのスタットビュー（Stat view）を「あーでもない，こーでもない」とメチャクチャに操作して，肩がコリながらやった覚えがあります．
ｔ検定などは平均値の差を検定するものですが，このウィルコクソンの符号付き順位和検定は「中央値」に差があるかを検定するもの，ということを聞きました．
当時は「何言ってんのか意味不明・・・」だったのですが，こうして手計算（エクセルだけど）したら意味もわかるというものです．
以下の記事を読んでも不安がある場合や，元の作業ファイルで確認したい場合は，
このリンク先→「統計記事のエクセルのファイル」から，
「ウィルコクソンの符号付順位和検定」
のエクセルファイルをダウンロードしてご確認ください．
では早速，
使うデータは以下のようなものです．
対応のあるt検定も同様ですが，並べる順番に気をつけてください．
対応のある検定データの検定ですから，各行で隣合うデータは「対応がある」状態にしておきます．
まず，このデータの差を算出します．
大したことではありません．引き算をするだけです．
次に，それぞれの「差」を絶対値にします．
「ABS」関数を使えば一気にできます．
この絶対値にした数列のところで，マン・ホイットニーのU検定の時のように，順位をつけます．
「RANK」関数を使うとよいでしょう．
昇順にして順位付けです．
ノンパラメトリック検定で注意しないといけないのは，同順位値が出た時ですね．
この場合，「4」が2ヶ所でみられます．
よって，4位と5位にあたる部分ですから，この2ヶ所の「4」を「4.5」にしておきます．
（こればっかりは手作業）
ウィルコクソンの “符号付き” 順位和検定ですから，「符号付け」作業をします．
上記のように，IF関数を使うのが便利です．
次は，その順位を2乗させます．
【順位】か【符号付】の列の数値に「^2」とすれば，一気に計算できます．
そして，【符号付】と【＾2】の列を合計します．
それぞれ，以下のような感じに．
上図は符号付の列，
下図は^2の列．
さて，
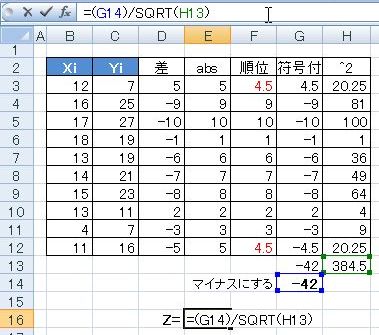
この例題では【符号付】の列の合計がマイナスになっているので，本来不要なのですが，この数値はマイナスにしとかなきゃいけないので，「マイナスにする」作業を入れときます．
あとで元データ（Xi，Yiの部分）をいじったとしても安心なように，これも「IF」関数を使って自動化しておきます．
さて，いよいよ統計量「Z」を算出です．
=(G14)/SQRT(H13)
このように，「マイナスにする」の数値と，「^2」の合計値をそれぞれ使用します．
最後に，の「Z」を使ってp値を算出です．
マン・ホイットニーのU検定でも使った，「NORMSDIST」関数を使います．
この関数の(ｚ)のところに，さっき出した「Z」の値を参照します．
=NORMSDIST(E16)*2
例のごとく，値を2倍しときます．
というわけで，この対応のある2群のデータには有意な差が認められました．
SPSSの計算結果も，
というように，同じになりました．
ウィルコクソンの符号付順位和検定で気をつけなければならない点をもう一つ．
以下の例でいうところの，D列12行目のように差がない（つまり差が０になる）データは順位付け作業に採用してはいけません．
ちなみに，以下の例では，【符号付】の合計値がプラスになっていますが，それをマイナスにしていることも確認しといてください．
これで対応のある２群のノンパラメトリック検定もエクセルでできるようになました．
多重比較検定をしたい場合は，
まずデータ間に有意性があるかどうかをフリードマンの検定で確認して，
■フリードマンの検定をエクセルでなんとかする
Amazon広告
その後，
■Excelで多重比較まとめ
■ノンパラメトリック検定で多重比較したいとき
を参照して検定してください．
手計算で算出するのが面倒な人は，思い切ってエクセル統計の購入をオススメします．
外部サイトにも有益なリストがあります．こちらも参考にしてください．
■大学生が自力で「統計学」の勉強をするための良書１０選
■1ヶ月で統計学入門したので「良かった本」と「学んだこと」のまとめ
ウィルコクソンの符号付き順位和検定ですが，私にとっては思い入れのある検定方法でして．
卒業論文の統計処理に採用した，私の論文初の検定方法です．
パラメトリック検定では有意性が認められないから 「どーしよー・・・」 と悩んでおり，指導教員の言われるがままにノンパラメトリック検定に鞍替えすることに．
マッキントッシュのスタットビュー（Stat view）を「あーでもない，こーでもない」とメチャクチャに操作して，肩がコリながらやった覚えがあります．
ｔ検定などは平均値の差を検定するものですが，このウィルコクソンの符号付き順位和検定は「中央値」に差があるかを検定するもの，ということを聞きました．
当時は「何言ってんのか意味不明・・・」だったのですが，こうして手計算（エクセルだけど）したら意味もわかるというものです．
以下の記事を読んでも不安がある場合や，元の作業ファイルで確認したい場合は，
このリンク先→「統計記事のエクセルのファイル」から，
「ウィルコクソンの符号付順位和検定」
のエクセルファイルをダウンロードしてご確認ください．
では早速，
使うデータは以下のようなものです．
対応のある検定データの検定ですから，各行で隣合うデータは「対応がある」状態にしておきます．
まず，このデータの差を算出します．
大したことではありません．引き算をするだけです．
「ABS」関数を使えば一気にできます．
「RANK」関数を使うとよいでしょう．
昇順にして順位付けです．
この場合，「4」が2ヶ所でみられます．
よって，4位と5位にあたる部分ですから，この2ヶ所の「4」を「4.5」にしておきます．
（こればっかりは手作業）
次は，その順位を2乗させます．
そして，【符号付】と【＾2】の列を合計します．
それぞれ，以下のような感じに．
下図は^2の列．
この例題では【符号付】の列の合計がマイナスになっているので，本来不要なのですが，この数値はマイナスにしとかなきゃいけないので，「マイナスにする」作業を入れときます．
=(G14)/SQRT(H13)
このように，「マイナスにする」の数値と，「^2」の合計値をそれぞれ使用します．
最後に，の「Z」を使ってp値を算出です．
この関数の(ｚ)のところに，さっき出した「Z」の値を参照します．
=NORMSDIST(E16)*2
例のごとく，値を2倍しときます．
SPSSの計算結果も，
ウィルコクソンの符号付順位和検定で気をつけなければならない点をもう一つ．
以下の例でいうところの，D列12行目のように差がない（つまり差が０になる）データは順位付け作業に採用してはいけません．
ちなみに，以下の例では，【符号付】の合計値がプラスになっていますが，それをマイナスにしていることも確認しといてください．
これで対応のある２群のノンパラメトリック検定もエクセルでできるようになました．
多重比較検定をしたい場合は，
まずデータ間に有意性があるかどうかをフリードマンの検定で確認して，
■フリードマンの検定をエクセルでなんとかする
Amazon広告
その後，
■Excelで多重比較まとめ
■ノンパラメトリック検定で多重比較したいとき
を参照して検定してください．
手計算で算出するのが面倒な人は，思い切ってエクセル統計の購入をオススメします．
※こんな怪しいブログよりも信頼性が高いものに触れてもらうよう，
■独学で統計処理作業をスキルアップさせるための本
という記事を書いています．参照してください．■独学で統計処理作業をスキルアップさせるための本
外部サイトにも有益なリストがあります．こちらも参考にしてください．
■大学生が自力で「統計学」の勉強をするための良書１０選
■1ヶ月で統計学入門したので「良かった本」と「学んだこと」のまとめ
