相関係数を理解する｜ウィキペディアを読んでもチンプンカンプンな人のための解説
詳しくはあとで勉強するから，とりあえず今は大事なところだけおさえておきたい
そんな人のための解説です．
学生に「ウィキペディアでも詳細なことを書いているから，それを読んで勉強しなさい」と言っても，そもそもウィキペディアに書いていることがチンプンカンプンという場合もあります．
こういう学生は，「じゃあ教科書を読みなさい」と言っても読まないことが多く，たいていネットで調べようとします（ネットですら調べないこともあるけど）．
なので，そんな「ネットに落ちている解説」としてここに述べたいと思うわけです．
では今回は「相関係数」について．
相関係数について，ウィキペディアでは以下のように解説しています．
■相関係数（Wikipedia）2019.12.9現在
相関係数（そうかんけいすう、英: correlation coefficient）は、2つの確率変数の間にある線形な関係の強弱を測る指標である。相関係数は無次元量で、−1以上1以下の実数に値をとる。相関係数が正のとき確率変数には正の相関が、負のとき確率変数には負の相関があるという。また相関係数が0のとき確率変数は無相関であるという。まあ，たしかによく分かりませんよね．
（中略）
普通、単に相関係数といえばピアソンの積率相関係数を指す。ピアソン積率相関係数の検定は偏差の正規分布を仮定する（パラメトリック）方法であるが、他にこのような仮定を置かないノンパラメトリックな方法として、スピアマンの順位相関係数、ケンドールの順位相関係数なども一般に用いられる。
（中略）
相関係数は、あくまでも確率変数の間にある線形な関係の尺度に過ぎない。また、確率変数間の因果関係を説明するものでもない。相関係数は順序尺度であり比尺度ではないので、例えば「相関係数が0.2と0.4であることから、後者は前者より2倍の相関がある」などと言うことはできない。
こういうのは正確な解説かもしれませんが，初学者が知りたいことではないのです．
相関係数は散布図で考える
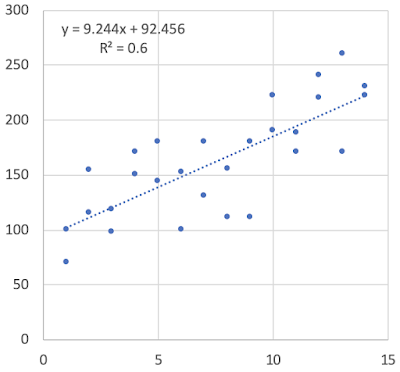
以下のような散布図がよく見られます．
論文などを読んでいても，よく目にすることが多いでしょう．
これは典型的な，
「横軸（X軸）が高値になるにつれて，縦軸（Y軸）も高値を示す」
という散布図です．
 |
| エクセルで作成した散布図 |
「横軸（X軸）が高値になるにつれて，縦軸（Y軸）も高値を示す」
という散布図です．
なお，相関係数は「ｒ」で示される数値です．
「ｒ＝0.8」とか，「ｒ＝0.43」などと書かれます．
ちなみに，エクセルの散布図の書式設定にある「R２」とは？
上記の図では，左上のところに「R２＝0.6」と書かれていますが，この「R２」というのは，エクセルの散布図の書式設定をした際に出てくるものです．
こういう画面のところで，チェックを入れると出てきますよね．
こういう画面のところで，チェックを入れると出てきますよね．
実は，この「R２」というのが，相関係数「ｒ」を二乗した値です．
上図では「R２＝0.6」となっていますので，「ｒ＝0.77」です．
エクセルで「相関係数」を算出するためには，「CORREL関数」または「PEARSON関数」を使います．
どちらも同じ値を得られます．
実は，この関数を使わなくても散布図のグラフ中に示された「R２」の平方根をとることで「相関係数（ｒ）」を出すことができます．
例えば，手元にある電卓（スマホのアプリでもいい）に0.6と入力してから「√（ルート）」マークを押してみてください．
「0.77459......」という数字が出ますね．
これが相関係数（つまりｒ）です．
この「R２」とは何なのか？ については，後半で説明します．
では，話を元に戻します．
指導教員から言われる，「相関係数は散布図を出して考えろ」の意味
上図の相関係数は「ｒ＝0.77（R２＝0.6）」ですが，データをちゃんと解釈するためには，この数値だけではダメなんです．なぜなら，同じ「ｒ＝0.77（R２＝0.6）」のデータとして，以下のようなものがあるからです．
「「R２値（ｒ値）」が一緒なのに，散布図がまったく違っていますね．
このデータの場合，右端に４個あるデータが飛び抜けており（外れ値），それに引っ張られてしまうことで「右肩あがり」のデータとして算出されています．
もしかすると，この４個のデータは特殊なものかもしれませんし，場合によっては入力ミスかもしれない．
つまり，前掲した散布図のように，
「横軸（X軸）が高値になるにつれて，縦軸（Y軸）も高値を示す」
とは言えない可能性があります．
例えば，試しに左下だけのデータで散布図を作ったら，以下のようになります．
このことを解説するために，ウィキペディアでは大げさな例が図示されています．
それがこちら．
この図の解説文として，ウィキペディアには以下のように述べられています．
「相関係数のことが理解できている人に分かる文章」
ですね．
これを初学者にも分かりやすく説明します．
「上段」のところは馴染みもあって理解しやすいかと思います．
相関係数というのは，
「データがなるべく直線的になった方が『強い相関』がある．つまり，１または−１に近づく」
というやつです．
逆に，円形に散布していると，それは「相関がない（ｒ＝０）」と言われます．
なお，相関係数の「ｒ値」による「相関の強さ」の解釈は，明確な基準はありません．
よく，ネットや教科書に以下のような表が紹介されていますよね．
※負の相関の場合は，ｒ値はマイナスにします．
でも，こういう基準はあくまでも目安であって，はっきり言えば，全くあてになりません．
なぜなら，まず第一の理由として，統計学的に「有意な相関係数」はデータ数（N数）によって違ってきます．
これはご存知の方も多いでしょう．
例えば，「ｒ＝0.5」という相関係数にしても，N数が20個の場合は５％水準で「有意」と判断されますが，10個の場合は有意ではなくなります．
※相関係数の有意性を知りたい場合は，
■エクセルで相関係数のｐ値を出す
を御覧ください．
さらに，研究領域によって相関係数の解釈は違ってきます．
例えば，「ｒ＝0.7」を強い相関だと解釈する場合もあれば，非常に弱い相関だと解釈する場合もあるからです．
ですが，「研究領域によって違う」と言われても，では自分の研究領域ではどうなのか？ が気になりますよね．
実はそれこそが，指導教員が「散布図で考えなさい」と言う理由です．
分かりやすい例を以下に示します．
以下の図は，ダイエット研究などで「サプリメント摂取量と体重減少量の相関関係」を調べたものとします．
R２値は0.49，つまり相関係数は0.7というものです．
この研究領域の場合だと，体重の減少量が２〜７ｋｇほどの幅があり，サプリメントを飲んだだけでその影響力があることを考えると，「ｒ＝0.7」というのは，極めて強い相関関係であると言えます．
一方，以下の場合はどうでしょうか．
この研究の場合は，新しく開発した測定装置を用いて，物の長さを推定できるという研究だったとしましょう．
そうすると，相関関係が0.7しかないのであれば，
「数センチ刻みの精度がほしい」
という測定装置の研究をしている場合は，とてもじゃないですが「高い精度で推定できている」とは言えません．
研究領域によって相関係数の解釈が異なるので，「散布図にして考えろ」というのは，そういうことです．
次に，ウィキペディアの図の「中段」について．
これはむしろ，「散布図だけ見て，早とちりしないように」ということです．
このような図のこと．
なんだか分かるようで分かりにくいものですが，具体的には以下のようなデータについてです．
例えば，勉強時間とテストの点数の関係について研究したところ，こんなデータが得られたとします．
このデータは，両グループで全く違う結果になっていますが，「相関係数（およびR２値）」は同じ値を示します．
つまり，
相関係数というのは，あくまでも横軸（X軸）と縦軸（Y軸）との間に生まれる関係性を分析しているので，その数値の大小までは反映されていませんよ．
ということです．
学生のレポートに見られるのですが，上記のような散布図を作って，
「青グループの相関係数はｒ＝0.95（R２値は0.9）であり，オレンジグループよりも勉強時間と点数の相関関係が高かった」
という誤解した文章を書いてくる人がいます．
ですが，相関係数でそこまでは分かりませんので注意してください．
（レポートだけじゃなく，たまに学術論文の査読をやっていても目にすることがあります．たぶん，指導教員が面倒をみてくれていない院生だと推察されます）
では最後に，以下の図で示されているものは何を意味しているのか？を解説します．
こういうやつですね．
いずれも奇妙な図形として散布されたデータですが，どれも「相関係数は０です」ってことを意味しています．
ウィキペディアでは面白可笑しく大げさに示していますが，実はこれ，データ解釈をする上では結構重要ですので，学生の皆さんはしっかり読んでおいてください．
具体的な事例として以下のようなデータがあったとします．
それは例えば，年齢別に何かのテストをやって，その得点を散布図にした研究です．
よくあるのが，もともとの研究者の思い込みがあって，
「年齢が高くなるにつれて，点数も高くなることを相関係数で示したかった」
という状況の場合，以下のような弱い相関係数になってしまったので，
「あぁ，もうちょっとキレイなデータだったら良かったのになぁ・・・」
っていうパターンがあるんです．
でもこれ，しっかりグラフを見れば，
「低年齢の頃に高くて，５歳くらいで最低値を見せ，そこから徐々に増加していく」
というUの字形のグラフにも見えるわけですよ．
前述のウィキペディアの図で言うところの，真ん中のやつですね．
こういうデータであれば，むしろ，
「どうして低年齢で点数が高くなるのか？ ５歳頃に低値を示すのはなぜか？」
という観点から研究できる可能性もあります．
他にも，ウィキペディアの図の右端みたいな図として，以下のような散布図になることもあります．
これを見て，
「めちゃくちゃなデータだな．年齢と点数に相関は無さそうだな」
と思ってしまいがちですが，実は各年齢で「高値グループ」と「低値グループ」に分けて分析できる可能性もあるわけです．
一般的には「決定係数」とか「寄与率」と呼ばれています．
前述したように，エクセルの散布図ではチェックを入れるだけでグラフ内に表示してくれる例のアレです．
ウィキペディアにも「決定係数」で解説されています．
■決定係数（Wikipedia）
例えば，上述したダイエット研究のデータ例をもう一度使って説明すると，「R２＝0.49」となっていますので，
「体重の減少にサプリメント摂取量の違いが４９％寄与している」
とか，
「ここで見られた体重の減少は，サプリメント摂取量の違いによって４９％が説明できる」
ということです．
逆に，説明できない割合，つまり「＝１ − R２」については，上記の例であれば，サプリメント摂取量の違い以外の「５１％」の「何か」が，体重減少を発生させていると解釈します．
それは例えば，運動実施や生活環境，体質的といったものが残りの５１％だと見做せます．
※ちなみに，上記の例データはとても非現実的なものなので，実際にサプリメントでダイエットできるとは思わないでくださいね．
これも質問として多いので「相関係数」から離れてしまいますが，書いておきます．
理系で数学が得意な学生にとっては「どうして分からないの？」というものでしょうが，これが何を意味しているのか分からない学生は意外と多いんです．
グラフの中に「 R２」と一緒にチェックを入れるところがあるやつ．
これのことです．
例えば，以下のようなデータ例があったとして，そこに，
「グラフに数式を表示する」
「グラフに R２を表示する」
を両方入れたとします．
そこに表示されている数式，
y = 1.6791 x + 23.112
なんのことはない，「一次関数」です．
あの「y = ax+b」という，中学数学のこと．
「数学」として勉強していた頃のものとは離れてしまうので，イメージしづらいのでしょう．
上記の例であれば，「正確だけど面倒なテスト」があったとして，これをもっと手軽に簡単にできる方法はないか？ という研究で用いられています．
例えば，一時期ＺＯＺＯＴＯＷＮがやっていたサービスに，人の体型を測るスーツがありましたよね．
■ZOZOSUITについて（ＺＯＺＯＴＯＷＮホームページより）
体型計測は，本来なら他の人の手で巻き尺や物差しを使って，時間をかけて計測するものですが，それを「着るだけ」でしかも一人で可能というものでした．
巻き尺を使った計測が「正確だけど面倒なテスト」，ゾゾスーツが「手軽で簡単なテスト」がそれに相当します．
同じ測定対象に，「正確だけど面倒なテスト」と「手軽で簡単なテスト」の両方で計測した結果，上記のようなデータが得られたします．
つまり，同じ人たちに対し，ゾゾスーツと巻き尺による実測の両方を計測したようなものです．
そして，「グラフに数式を表示する」で得られた一次関数を使えば，「手軽で簡単なテスト」の結果をもとに，「正確だけど面倒なテスト」による結果を推定することができます．
例えば，手軽で簡単なテストの結果（X）が「１００」であれば，
y = 1.6791 × 100 + 23.112
を計算することで，Yの値である「正確だけど面倒なテスト」の得点を，
ｙ＝ 191.022（およそ191点）
として算出することができます．
関連記事
■卒論・修論のための「統計」の部分の書き方
■【やってはいけない】卒論・ゼミ論を１日で書く方法
■【卒論・ゼミ論】絶望的な君が無理矢理「急成長」する方法
■卒論・ゼミ論で統計学的有意差が出なくて困っている時に読むブログ記事
■ｔ検定：対応ある／なしの違いは何か
■アンケートだけで卒論・修論を乗り切るためのエクセルｔ検定
■アンケートだけで卒論・修論を乗り切るためのエクセルχ二乗検定
■エクセルで相関係数のｐ値を出す
■エクセルでの簡単統計（相関関係）
それがこちら．
この図の解説文として，ウィキペディアには以下のように述べられています．
(x, y) の組とそれぞれの相関係数を示している。相関は非線形性および直線関係の向きを反映するが（上段）、その関係の傾きや（中段）、非直線関係の多くの面も反映しない（下段）。中央の図の傾きは0であるが、この場合はYの分散が0であるため相関係数は定義されない。いわゆる，
「相関係数のことが理解できている人に分かる文章」
ですね．
これを初学者にも分かりやすく説明します．
「上段」のところは馴染みもあって理解しやすいかと思います．
相関係数というのは，
「データがなるべく直線的になった方が『強い相関』がある．つまり，１または−１に近づく」
というやつです．
逆に，円形に散布していると，それは「相関がない（ｒ＝０）」と言われます．
なお，相関係数の「ｒ値」による「相関の強さ」の解釈は，明確な基準はありません．
よく，ネットや教科書に以下のような表が紹介されていますよね．
※負の相関の場合は，ｒ値はマイナスにします．
 |
| Cohen, J. (1988) |
なぜなら，まず第一の理由として，統計学的に「有意な相関係数」はデータ数（N数）によって違ってきます．
これはご存知の方も多いでしょう．
例えば，「ｒ＝0.5」という相関係数にしても，N数が20個の場合は５％水準で「有意」と判断されますが，10個の場合は有意ではなくなります．
※相関係数の有意性を知りたい場合は，
■エクセルで相関係数のｐ値を出す
を御覧ください．
さらに，研究領域によって相関係数の解釈は違ってきます．
例えば，「ｒ＝0.7」を強い相関だと解釈する場合もあれば，非常に弱い相関だと解釈する場合もあるからです．
ですが，「研究領域によって違う」と言われても，では自分の研究領域ではどうなのか？ が気になりますよね．
実はそれこそが，指導教員が「散布図で考えなさい」と言う理由です．
分かりやすい例を以下に示します．
以下の図は，ダイエット研究などで「サプリメント摂取量と体重減少量の相関関係」を調べたものとします．
R２値は0.49，つまり相関係数は0.7というものです．
この研究領域の場合だと，体重の減少量が２〜７ｋｇほどの幅があり，サプリメントを飲んだだけでその影響力があることを考えると，「ｒ＝0.7」というのは，極めて強い相関関係であると言えます．
一方，以下の場合はどうでしょうか．
この研究の場合は，新しく開発した測定装置を用いて，物の長さを推定できるという研究だったとしましょう．
そうすると，相関関係が0.7しかないのであれば，
「数センチ刻みの精度がほしい」
という測定装置の研究をしている場合は，とてもじゃないですが「高い精度で推定できている」とは言えません．
研究領域によって相関係数の解釈が異なるので，「散布図にして考えろ」というのは，そういうことです．
次に，ウィキペディアの図の「中段」について．
これはむしろ，「散布図だけ見て，早とちりしないように」ということです．
このような図のこと．
なんだか分かるようで分かりにくいものですが，具体的には以下のようなデータについてです．
例えば，勉強時間とテストの点数の関係について研究したところ，こんなデータが得られたとします．
つまり，
相関係数というのは，あくまでも横軸（X軸）と縦軸（Y軸）との間に生まれる関係性を分析しているので，その数値の大小までは反映されていませんよ．
ということです．
学生のレポートに見られるのですが，上記のような散布図を作って，
「青グループの相関係数はｒ＝0.95（R２値は0.9）であり，オレンジグループよりも勉強時間と点数の相関関係が高かった」
という誤解した文章を書いてくる人がいます．
ですが，相関係数でそこまでは分かりませんので注意してください．
（レポートだけじゃなく，たまに学術論文の査読をやっていても目にすることがあります．たぶん，指導教員が面倒をみてくれていない院生だと推察されます）
では最後に，以下の図で示されているものは何を意味しているのか？を解説します．
こういうやつですね．
いずれも奇妙な図形として散布されたデータですが，どれも「相関係数は０です」ってことを意味しています．
ウィキペディアでは面白可笑しく大げさに示していますが，実はこれ，データ解釈をする上では結構重要ですので，学生の皆さんはしっかり読んでおいてください．
具体的な事例として以下のようなデータがあったとします．
それは例えば，年齢別に何かのテストをやって，その得点を散布図にした研究です．
よくあるのが，もともとの研究者の思い込みがあって，
「年齢が高くなるにつれて，点数も高くなることを相関係数で示したかった」
という状況の場合，以下のような弱い相関係数になってしまったので，
「あぁ，もうちょっとキレイなデータだったら良かったのになぁ・・・」
っていうパターンがあるんです．
「低年齢の頃に高くて，５歳くらいで最低値を見せ，そこから徐々に増加していく」
というUの字形のグラフにも見えるわけですよ．
前述のウィキペディアの図で言うところの，真ん中のやつですね．
こういうデータであれば，むしろ，
「どうして低年齢で点数が高くなるのか？ ５歳頃に低値を示すのはなぜか？」
という観点から研究できる可能性もあります．
他にも，ウィキペディアの図の右端みたいな図として，以下のような散布図になることもあります．
「めちゃくちゃなデータだな．年齢と点数に相関は無さそうだな」
と思ってしまいがちですが，実は各年齢で「高値グループ」と「低値グループ」に分けて分析できる可能性もあるわけです．
ところで，R２値ってなんですか？
一般的には「決定係数」とか「寄与率」と呼ばれています．
前述したように，エクセルの散布図ではチェックを入れるだけでグラフ内に表示してくれる例のアレです．
ウィキペディアにも「決定係数」で解説されています．
■決定係数（Wikipedia）
決定係数（けっていけいすう、英: coefficient of determination、R2）は、統計学において、独立変数（説明変数）が従属変数（目的変数）のどれくらいを説明できるかを表す値である。寄与率と呼ばれることもある。標本値から求めた回帰方程式（モデル）のあてはまりの良さの尺度として利用される。
例えば，上述したダイエット研究のデータ例をもう一度使って説明すると，「R２＝0.49」となっていますので，
「体重の減少にサプリメント摂取量の違いが４９％寄与している」
とか，
「ここで見られた体重の減少は，サプリメント摂取量の違いによって４９％が説明できる」
ということです．
それは例えば，運動実施や生活環境，体質的といったものが残りの５１％だと見做せます．
※ちなみに，上記の例データはとても非現実的なものなので，実際にサプリメントでダイエットできるとは思わないでくださいね．
最後に，「グラフに数式を表示する」の数式ってなに？
これも質問として多いので「相関係数」から離れてしまいますが，書いておきます．
理系で数学が得意な学生にとっては「どうして分からないの？」というものでしょうが，これが何を意味しているのか分からない学生は意外と多いんです．
グラフの中に「 R２」と一緒にチェックを入れるところがあるやつ．
これのことです．
例えば，以下のようなデータ例があったとして，そこに，
「グラフに数式を表示する」
「グラフに R２を表示する」
を両方入れたとします．
y = 1.6791 x + 23.112
なんのことはない，「一次関数」です．
あの「y = ax+b」という，中学数学のこと．
「数学」として勉強していた頃のものとは離れてしまうので，イメージしづらいのでしょう．
上記の例であれば，「正確だけど面倒なテスト」があったとして，これをもっと手軽に簡単にできる方法はないか？ という研究で用いられています．
例えば，一時期ＺＯＺＯＴＯＷＮがやっていたサービスに，人の体型を測るスーツがありましたよね．
■ZOZOSUITについて（ＺＯＺＯＴＯＷＮホームページより）
体型計測は，本来なら他の人の手で巻き尺や物差しを使って，時間をかけて計測するものですが，それを「着るだけ」でしかも一人で可能というものでした．
巻き尺を使った計測が「正確だけど面倒なテスト」，ゾゾスーツが「手軽で簡単なテスト」がそれに相当します．
同じ測定対象に，「正確だけど面倒なテスト」と「手軽で簡単なテスト」の両方で計測した結果，上記のようなデータが得られたします．
つまり，同じ人たちに対し，ゾゾスーツと巻き尺による実測の両方を計測したようなものです．
そして，「グラフに数式を表示する」で得られた一次関数を使えば，「手軽で簡単なテスト」の結果をもとに，「正確だけど面倒なテスト」による結果を推定することができます．
例えば，手軽で簡単なテストの結果（X）が「１００」であれば，
y = 1.6791 × 100 + 23.112
を計算することで，Yの値である「正確だけど面倒なテスト」の得点を，
ｙ＝ 191.022（およそ191点）
として算出することができます．
関連記事
■卒論・修論のための「統計」の部分の書き方
■【やってはいけない】卒論・ゼミ論を１日で書く方法
■【卒論・ゼミ論】絶望的な君が無理矢理「急成長」する方法
■卒論・ゼミ論で統計学的有意差が出なくて困っている時に読むブログ記事
■ｔ検定：対応ある／なしの違いは何か
■アンケートだけで卒論・修論を乗り切るためのエクセルｔ検定
■アンケートだけで卒論・修論を乗り切るためのエクセルχ二乗検定
■エクセルで相関係数のｐ値を出す
■エクセルでの簡単統計（相関関係）
コメント
コメントを投稿
常識の範疇でご記入ください。お問い合わせはメールでも受け付けています。その場合は「プロフィール」からお願いします。